분류 전체보기
-
Monty Hall 몬티홀 C언어로 확인해보기2020.10.04
Monty Hall 몬티홀 C언어로 확인해보기
몬티홀을 처음 들었던 것은 지난 겨울이다. 부모님과 스키장을 갔었는데, 리프트를 타고 올라가는 시간이 꽤 걸리다보니 그 때 부모님과 대화를 하면서 시간을 보냈었다. 그 때 아버지가 처음 몬티홀에 대해 말씀해주셨었다. 당시에 나는 이해가 되지 않았고 스키를 타는 내내 몬티홀 생각에 빠져 있었다. 그리고 시간이 조금 흘러 유튜브 추천 영상에 평소에 내가 좋아하던 유투버 우왁굳의 몬티홀 관련 영상이 올라와서 봤다.
이외에도 여러 몬티홀 영상을 찾아보면서 신기하다고 느꼈다. 그리고 내가 직접 알아봐야겠다고 생각해서 C언어(C++)로 작성해보기로 했다. 작성은 C++로 했는데 거의 99% C언어와 같이 쓰여서 C언어만 알아도 아래 코드를 거의 이해할 수 있을 것이다.
#include <iostream>
#include <time.h>
using namespace std;
int main() {
int user, random, user2;
bool one = false, two = false, three = false;
float cnt = 0, correct = 0, wrong = 0;
srand(time(NULL));
cout << "Welcome to Monty Hall Problem\n\n";
while(true){
cnt++;
/*초기화*/
one = false;
two = false;
three = false;
random = rand() % 3 + 1; // 랜덤하게 1번, 2번, 3번 문 중 어느 곳에 슈퍼카가 있을지 선택
switch (random) {
case 1:
one = true;
break;
case 2:
two = true;
break;
case 3:
three = true;
break;
}
cout << "1, 2, 3 번 문이 있습니다. 한 곳에는 슈퍼카가, 나머지 두 곳에는 염소가 있습니다.\n1, 2, 3번 문 중 어떤 것을 고르시겠습니까?\n=>";
cin >> user; // 사용자로부터 어떤 문을 선택할지 입력받습니다.
if (one == false && user != 1) {
cout << "1번에는 염소가 있습니다.\n";
if (user == 2) {
cout << "새로 선택할 번호를 입력해주세요, 그대로 진행하시려면 원래 선택했던 번호를 입력해주세요.\n";
}
else if (user == 3) {
cout << "새로 선택할 번호를 입력해주세요, 그대로 진행하시려면 원래 선택했던 번호를 입력해주세요.\n";
}
}
else if (two == false && user != 2) {
cout << "2번에는 염소가 있습니다.\n";
if (user == 1) {
cout << "새로 선택할 번호를 입력해주세요, 그대로 진행하시려면 원래 선택했던 번호를 입력해주세요.\n";
}
else if (user == 3) {
cout << "새로 선택할 번호를 입력해주세요, 그대로 진행하시려면 원래 선택했던 번호를 입력해주세요.\n";
}
}
else if (three == false && user != 3) {
cout << "3번에는 염소가 있습니다.\n";
if (user == 2) {
cout << "새로 선택할 번호를 입력해주세요, 그대로 진행하시려면 원래 선택했던 번호를 입력해주세요.\n";
}
else if (user == 1) {
cout << "새로 선택할 번호를 입력해주세요, 그대로 진행하시려면 원래 선택했던 번호를 입력해주세요.\n";
}
}
cin >> user2;//사용자가 바꿀 것인지 확인해봅니다.
if ((user2 == 1 && one == true)||(user2 == 2 && two == true)||(user2 == 3 && three == true)) {
cout << "***슈퍼카를 획득하셨습니다! 축하드립니다.***\n\n";
correct++;
}
else {
cout << "아쉽게도 " << user2 << "에는 염소가 있습니다.\n\n";
wrong++;
}
/*지금까지의 결과를 출력합니다.*/
cout << "시도 횟수 : " << cnt << "\n";
cout << "맞춘 횟수 : " << correct << "\n";
cout << "틀린 횟수 : " << wrong << "\n";
cout << "지금까지 맞춘 확률 " << (correct / cnt) * 100 << "%\n\n\n";
}
}
실험은 다음과 같이 진행됐다.
- 실험1
처음 선택했던 값을 바꿔서 선택한다. 이 행위를 총 100번 반복한 후 확률을 확인해본다.
- 실험2
처음 선택했던 값을 바꾸지 않는다. 이 행위를 총 100번 반복한 후 확률을 확인해본다.
원래 이론대로라면 실험1로 슈퍼카를 얻을 확률은 66.666...%에 가까워야 하고, 실험2로 슈퍼카를 얻을 확률은 66.6666....%에 가까워야 한다.
매우 간단하게 이론 설명을 하자면,
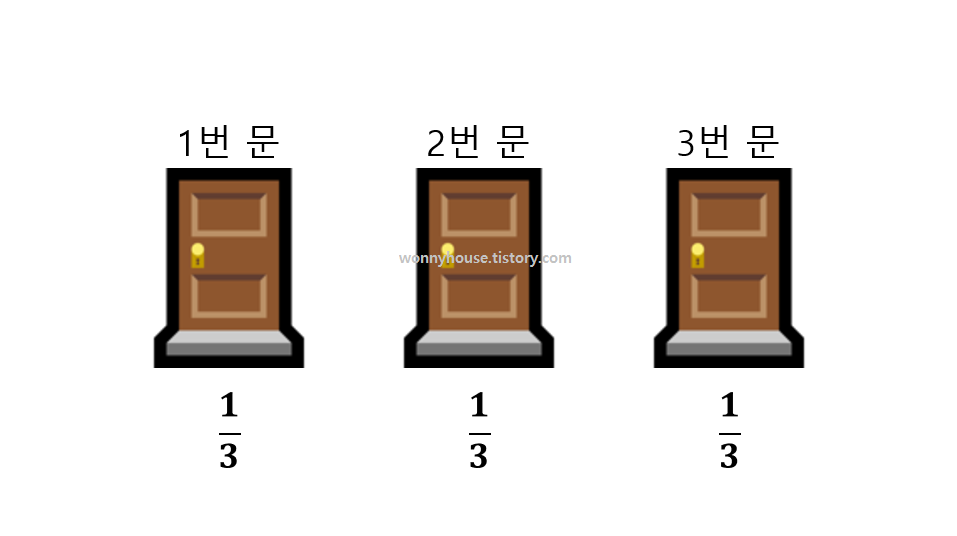
이렇게 세 개의 문이 있다. 세 문 중 한 곳에 슈퍼카가 있고, 나머지 두 곳에 염소가 한마리씩 있다.

그리고 예를 들어서 1번 문을 선택했다고 생각해보자. 내가 선택한 문에 슈퍼카가 있을 확률은 1/3이고, 나머지 두 문 중에 있을 확률은 2/3이다.
그런데 이 때, 사회자가 3번문에 염소가 있다고 하면서 3번 문을 열어줬다. 그리고 아래처럼 염소가 나왔다.

그러면 자동으로 2번 문의 확률은 2/3가 되면서 2번 문에 슈퍼카가 있을 확률이 더 높아진다. 나는 이렇게 이해를 하고 이해를 못했다.(?) 그래서 직접 코드로 작성해보고 내가 두 눈으로 실험을 해보자고 생각했고 위 코드대로 작성했고 실험을 시작했다. 다시 실험 내용을 한 번 더 적으면 아래와 같다.
실험은 다음과 같이 진행됐다.
- 실험1
처음 선택했던 값을 바꿔서 선택한다. 이 행위를 총 100번 반복한 후 확률을 확인해본다.
- 실험2
처음 선택했던 값을 바꾸지 않는다. 이 행위를 총 100번 반복한 후 확률을 확인해본다.
* 몬티홀을 믿고 선택한 값을 바꾸는 실험 1 결과, 100회 진행



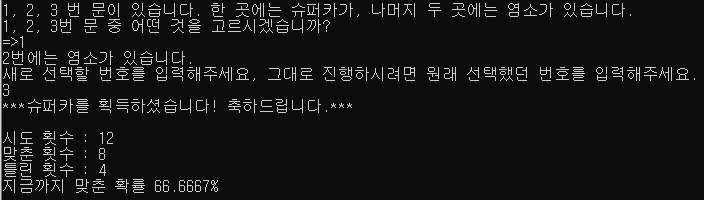

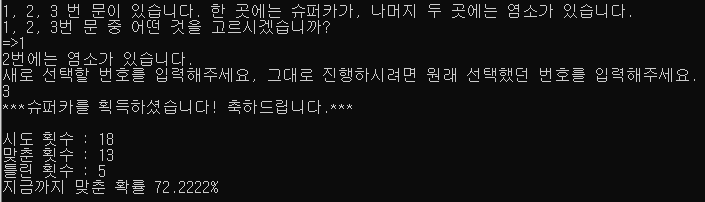



66.66%에 근접한 68%가 나왔다. 믿기지 않았다. 그니까 바꾸는 것이 슈퍼카를 얻을 수 있는 확률이 더 높게 나온 것이다.ㄷㄷ 또한 15회까지 3의 배수일 때마다 정확히 66.6666%가 나왔다.
사실 여기까지만 진행해보려고 했는데 반대로 해도 정말 33.33%에 가까운 값이 나올지 궁금해서 실험을 진행해봤다.
* 몬티홀보다는 나를 믿고 선택한 값을 바꾸지 않는 실험 2 결과, 실험 1과 마찬가지로 100회 진행




실험2, 100회의 결과는 36%. 이론대로라면 33.3333%였는데, 그래도 근접한 확률이 나왔다. 이 실험을 통해서 내가 깨달은 것은 자신을 믿지 않고 몬티홀을 믿으면 슈퍼카를 얻을 수 있는 확률이 32%가 높다는 것이다. 그러나 슈퍼카가 나오지 않았을 때 몬티홀은 책임을 져주지 않는다.
더 나아가서 100개의 문이 있고, 내가 선택한 한 개의 문을 제외하고 98개의 문을 열어서 염소를 보여준다면, 기존에 내가 선택한 문에 슈퍼카가 있을 확률은 1/100이고, 나머지 열지 않은 한 문에 슈퍼카가 있을 확률은 99/100이다. 신기하다. 신기한데 뭔가 찜찜하다. 정말 이게 맞는다는 것이 뭔가 찜찜하다. 그냥 1/2일 것 같은데...
찜찜한 실험 끝
'프로그래밍 > C,C++' 카테고리의 다른 글
| 부동소수점의 비교연산 안되는 이유 및 오차범위 해결하기 (0) | 2020.10.10 |
|---|---|
| 백준 11650 C++ 및 vector container, pair, sort, 범위 기반 for문 (0) | 2020.08.03 |
| C++ Getter and setter (0) | 2020.03.17 |
| C++ Object Functions(클래스 함수) (0) | 2020.03.17 |
| C++ 클래스(class)와 생성자(constructor) (0) | 2020.03.17 |